Latviešu valodas versija nav pieejama

The macroeconomic impact of changes in economic bank capital buffers

Prepared by Derrick Kanngiesser, Reiner Martin, Diego Moccero and Laurent Maurin

How do changes in bank capital requirements affect bank lending, lending spreads and the broader macroeconomy? The answer to this question is important for calibrating and assessing macroprudential policies. There is, however, relatively little empirical evidence to answer this question in the case of the euro area countries. This article contributes to filling this gap by studying the effects of changes in economic bank capital buffers in the four largest euro area countries. We use bank-level data and macroeconomic information to estimate a bank-internal, target level of economic capital ratio, i.e. the capital ratio that a bank would like to hold considering its own characteristics (size, profitability, risk aversion of its creditors, risk exposure, etc.) and macroeconomic conditions (expected GDP growth, etc.). Economic bank capital buffers are then computed as the difference between the current and the target economic capital ratio. However, due to adjustment costs, banks cannot adjust the actual capital ratio to the target level instantaneously. As a result, a change in the target capital ratio will result in an instantaneous change in the economic capital buffer. These buffers are aggregated at the country level and included in a panel Bayesian vector auto regressive (VAR) model. With the VAR, it is then possible to compute the response of macroeconomic and banking variables to a change in the buffer. The idea is that changes in economic capital buffers mimic the effects a change in regulatory capital requirements would have on the economy. We find that a negative economic capital buffer shock, i.e. a decline in actual capital ratios below the target level, leads to a modest decline in output and prices and to a larger decline in bank lending growth. By affecting the difference between actual and target economic capital ratios, these findings suggest that countercyclical capital-based macroprudential policy measures can be useful to dampen the financial cycle.

1 Introduction

The global financial crisis revealed a need for macroprudential policy tools to mitigate the build-up of risk in the financial system and to enhance the resilience of financial institutions. Consequently, macroprudential policy has received increasing attention and macroprudential action has been taken in many jurisdictions, including the countries of the euro area. Many macroprudential measures take the form of capital-based instruments, aimed at increasing banks' resilience to macro-financial shocks and limiting procyclicality and excessive amplification of the financial cycle. Capital-based measures include the countercyclical capital buffer (CCyB), the systemic risk buffer (SRB) and capital buffers for systemically important institutions (Kok et al., 2014).

Estimating the impact of shocks to bank capital ratios is important for calibrating and assessing macroprudential policies. The idea behind countercyclical capital buffers, in particular, is to impose a capital surcharge on banks in order to limit the excessive amplification of credit cycles and to incentivise banks to build up capital so that they are better prepared to withstand losses in an economic downturn. This leads to the questions of whether, and to what extent, changes in capital ratios affect bank lending, lending spreads and the broader macroeconomy. Answering these questions is not straightforward, given that capital ratios are endogenously determined and influenced by various factors including demand conditions, as well as by discretionary changes in policy (e.g. monetary policy, supervisory actions, etc.). Furthermore, the empirical evidence with the macroprudential use of CCyBs in the euro area is still relatively limited.^[1]

This article estimates the impact of shocks to economic bank capital buffers on banking and macroeconomic variables in four large euro area countries (Germany, Spain, France and Italy).^[2] As mentioned before, the limited use of the CCyB in euro area countries prevents the implementation of a proper time series econometric analysis to test its impact on bank lending and the economy. However, one can estimate the impact of changes in capital ratios based on the notion of the target economic capital ratio, i.e. the capital ratio that a bank would like to hold considering its own characteristics (size, profitability, risk aversion of its creditors, risk exposure, etc.) and macroeconomic conditions (expected GDP growth, etc.). The target economic capital can also be affected by capital requirements, as found for the United Kingdom by Francis and Osborn (2009).^[3] Unfortunately, such series are available only over a very short period of time for the countries and banks under consideration, hence preventing its use in time series econometric analysis. In turn, an economic bank capital buffer can be computed as the difference between the actual and the target level of the economic capital ratio. In particular, we follow Mésonnier and Stevanovic (2017) and compute economic bank capital buffers for large stock-exchange listed euro area banks. Next, country-level aggregates are computed as a weighted average of the bank-level buffers. When economic capital buffers are positive and large, banks have room to finance the economy. However, when economic capital buffers are negative, banks may need to curtail lending and/or increase the pricing of loans for actual capital ratios to reach the target in the future. Country-level buffers are then included in a vector auto regressive (VAR) model, together with other macroeconomic (policy interest rate, growth in economic activity and rate of inflation) and banking sector variables (growth rates of bank lending to households and non-financial corporations and bank lending spreads) in order to identify the effects of exogenous changes in these capital buffers. The idea is that changes in economic capital buffers mimic the effects a change in regulatory capital requirements would have on the economy.

2 Challenges in estimating the impact of changes in bank capital buffers

Identifying the economic impact of changes in bank capital ratios is challenging because bank capital itself tends to respond to changes in bank lending and the macroeconomic environment. A large part of the variation in bank capital is likely to result from variations in macroeconomic variables (such as changes in economic activity and interest rate spreads), as well as from changes in economic policy per se. For example, changes in macroeconomic variables affect capital through operating income and asset valuation. The literature deals with this endogeneity issue in three ways.

A first strand of literature has tried to isolate “true” shocks to bank capital, e.g. those stemming from losses associated with declines in real estate prices or losses arising from exposures to third countries. For example, Bernanke and Lown (1991) find that a shortage of equity capital due to the bursting of a real estate bubble played a role during the credit crunch observed in the early 1990s in the United States. Peek and Rosengren (1997) found that Japanese bank branches’ lending to US non-financial corporations declined in response to heavy losses in their parents’ capital positions associated with the sharp decline in Japanese stock markets in the early 1990s. Watanabe (2007) also studied the case of Japan in the late 1990s and found that banks cut back on their lending supply in response to the large loss of bank capital associated with write-offs of non-performing loans in the real estate sector.

A second strand of the literature seeks to identify regulatory or supervisory shocks to bank capital, where banks are required by a regulatory or supervisory authority to hold higher capital ratios. Such shocks may be bank-specific or system-wide and are in some cases introduced over a transition period to allow for a smooth implementation and avoid unintended, short-term negative effects. Several studies have looked at the United Kingdom, where the regulators have imposed time-varying, bank-specific capital requirements since Basel I.^[4] These studies show that more stringent capital requirements, while producing significant benefits such as greater financial stability and a lower probability of crisis events, may also have costs in terms of reduced loan supply, at least in the short term (Francis and Osborne, 2009; Aiyar et al., 2014; Bridges et al., 2014). In the euro area, Jiménez et al. (2017), looking at the experience with the Spanish dynamic provisioning framework, found that countercyclical dynamic provisioning helps to smooth credit supply cycles. Mésonnier and Monks (2015) and Gropp et al. (2016) find evidence suggesting that banks that had to increase capital ratios in the context of the 2011 EBA recapitalisation exercise increased their ratios by curtailing their lending supply, rather than by raising the level of capital.

A major drawback of the studies mentioned so far is that they tend to focus on specific, one-off events and neglect the dynamic interaction and feedback effects between banking variables and macroeconomic variables. Specific one-off events are difficult to generalise. Moreover, these studies are mainly based on single equation modelling frameworks, neglecting the dynamic interaction among banks’ asset categories, possibly assuming exogeneity across variables. Since the studies tend to focus on capital shocks to individual banks, they are ill-equipped to analyse the feedback loop between bank capital shocks and the macroeconomy. This feedback loop is, however, expected to play an important role when many banks face simultaneous and correlated changes in capital owing to regulatory changes, cyclical conditions, or the need to strengthen their capital base to regain market confidence.

As a result, a third strand of literature has estimated the impact of bank capital shocks by including aggregate bank ratios or buffers in macroeconometric models with a broader set of banking and macroeconomic variables. This strand of literature includes Hancock et al. (1995), Lown and Morgan (2006), Berrospide and Edge (2010), Kok et al. (2016), Noss and Toffano (2016), Meeks (2017) and Mésonnier and Stevanovic (2017) and Kanngiesser et al. (2017). All of these studies focus on the United States or the United Kingdom, with the exception of Kok et al. (2016) and Kanngiesser et al. (2017), who study European economies and the euro area, respectively. They find that shocks to bank capital tend to depress bank lending, increase lending spreads and hamper economic activity. This article follows this strand of literature and uses a capital buffer, rather than the actual capital ratio (as in Kok et al., 2016, and Kanngiesser et al., 2017), to identify the impact of shocks to bank capital in euro area countries.

3 Estimating economic bank capital buffers for euro area countries

The first step in the estimation of the impact of changes in economic banks’ capital buffers on banking variables and the macroeconomy is to estimate economic capital buffers per se. It is assumed that banks adjust their capital ratios towards a pre-specified or target level of economic capital ratio. The target level of economic capital ratio is the capital ratio that banks would like to hold considering their own characteristics and macroeconomic conditions.^[5] However, owing to adjustment costs, a bank will adjust its actual capital ratio only slowly towards its desired target. See Box 1 for more details regarding the partial adjustment model used to estimate the target level of economic capital ratio.^[6]

The target level of economic bank capital is assumed to fluctuate with banks’ characteristics and the business and financial cycle. Characteristics that affect the target level of economic capital in individual banks include banks’ total assets, their annual stock price growth rate and the volatility of each bank’s stock price. The first bank-level variable captures bank size, the second is a measure of bank profitability and the third reflects uncertainty to generate profits. These bank-level variables are standard determinants of bank capital ratios in the empirical literature.^[7] At the same time, target capital ratios are assumed to be chosen for the purpose of absorbing expected future losses. As such, macroeconomic information relevant for assessing the probability of future losses is also considered in the regression. In particular, key macroeconomic variables that may affect how much capital a bank would like to hold to absorb future losses are the one-year ahead real GDP growth forecast for the country where the bank is located, the sovereign bond yield spread of that country and a euro area aggregate corporate bond high yield spread (the latter two variables reflect the opportunity cost of capital).

Economic bank capital buffers are a good indicator for capturing banks’ constraints in providing lending to the economy. Economic bank capital buffers are computed as the difference between the actual and the target economic capital ratio (country-level capital buffers are computed as a weighted average, using total assets, of the bank-level buffers). When actual capital ratios are above the target (positive buffer), banks have room to keep expanding and lending more to the economy. However, when the target capital ratio is above the actual ratio (negative buffer), banks may need to adjust lending (and the pricing of loans) in order to attain the target economic capital level.

Aggregate economic bank capital buffers for the four countries under consideration fluctuated considerably during the period covered in this article, namely between the first quarter of 2005 and the fourth quarter of 2018 (see Chart 1). The buffers started to decline during the period of economic expansion from 2005‑07 and declined strongly at the height of the international financial crisis (2009 and 2010). After recovering briefly, the buffers declined again during the euro area sovereign debt crisis in 2012. Subsequently, the buffers narrowed and turned positive towards the end of the review period. These developments are in line with the observed increase in actual bank capital ratios.

Chart 1

Economic bank capital buffers fluctuated largely since 2005

Sources: DataStream, ECB and Eurostat.
Notes: The capital buffer is defined in percentages. The sample spans the period from the first quarter of 2005 to the fourth quarter of 2018.

Chart 2

Macroeconomic and banking variables deteriorated during the international financial crisis and the euro area sovereign debt crisis, together with the decline in economic bank capital buffers

Sources: ECB and Eurostat.
Notes: Real GDP growth, inflation and corporate and mortgage lending are computed as the log difference of the respective variable multiplied by 100. The corporate and mortgage spreads are defined in percentages. The sample spans the period from the first quarter of 2005 to the fourth quarter of 2018.

4 The macroeconomic impact of shocks to economic bank capital buffers

The evolution of bank lending volumes and spreads in the four countries under consideration suggests that economic bank capital buffers may have played an important role in shaping these variables (see Charts 1 and 2). In particular, mortgage and corporate lending decelerated substantially during the international financial crisis and then again during the euro area sovereign debt crisis. In both periods, bank lending spreads widened. As a result of the collapse in bank lending and soaring bank lending spreads, economic activity deteriorated. The concomitant decline in economic bank capital buffers, which capture constraints in the ability of banks to provide lending to the economy, offers prima facie evidence of the potential impact of changes in economic bank capital buffers on macroeconomic and banking variables.

However, the simple evolution of the variables in Charts 1 and 2 does not allow the disentangling of the particular drivers of bank lending and lending spreads. On the one hand, the drop in bank lending growth coincided with an economic downturn, pointing to demand factors affecting lending. On the other hand, it is likely that the decline in bank capital buffers led banks to curtail lending to households and corporations and to increase lending spreads. More expensive and less buoyant lending then contributed to the further slowdown observed in economic activity and inflation. As such, a macroeconometric model is needed to disentangle the impact of shocks to economic banks’ capital buffers from other sources of variation in bank lending and lending spreads.

We use a panel Bayesian VAR model to quantify the impact of changes in bank capital buffers on banking variables and the macroeconomy in the four euro area countries.^[8] The starting point in the analysis is the standard VAR model used extensively in monetary policy analysis (including the monetary policy interest rate, economic activity and inflation), extended to include aggregate banking variables (bank lending volumes and spreads) on top of the country-level bank capital buffers.^[9] Based on this model, it is possible to estimate the response of the variables to a negative shock in bank capital buffers, i.e. a decline in actual capital ratios below the target value.^[10]

A negative capital buffer shock leads to a modest decline in output and prices and to a larger decline in bank lending growth (see Chart 3). The source of this shock could be an increase in capital requirements (e.g. the CCyB) that increases the target economic capital ratio of the banks.^[11] As a result, the banks adjust their balance sheets (lending) in order for the actual capital ratio to converge to the target in the future. Indeed, the cumulative decline in corporate lending nine quarters after the shock (when the trough is reached) ranges from 0.4 percentage points in Germany to 2.6 percentage points in Italy and, for mortgage lending, from 0.5 to 3.6 percentage points, respectively. The impact on bank lending spreads peaks at three quarters after the shock but is very small or insignificant (smaller than 0.1 percentage points in all of the countries). The curtailing of lending has macroeconomic implications. The estimated cumulative impact on real GDP growth over nine quarters is very small in Germany (-0.07 percentage points), while it is strongest in Italy (-0.9 percentage points).

Chart 3

Dynamic responses of endogenous variables to a one standard deviation shock to economic bank capital buffers

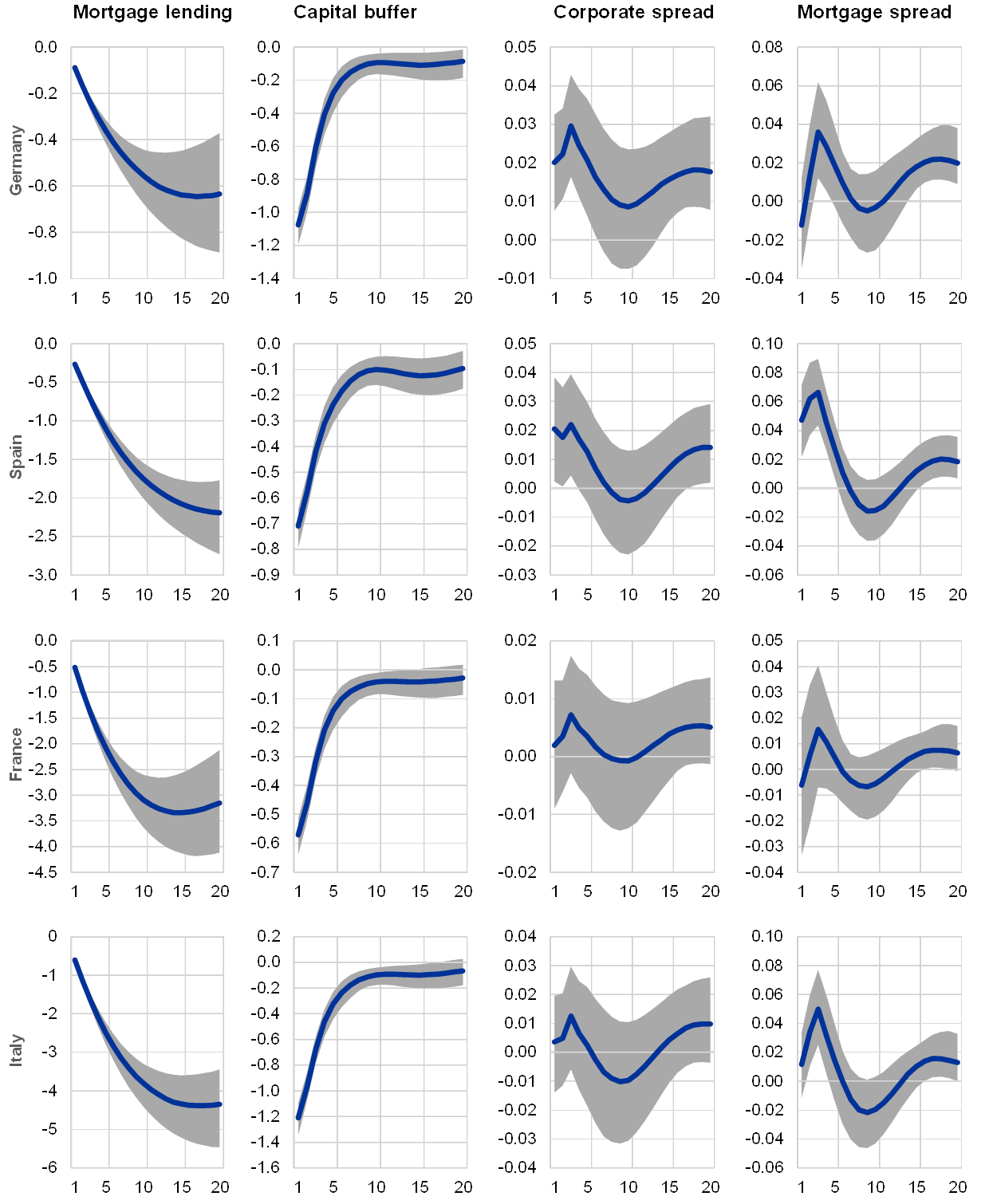
Notes: The impulse response functions (IRFs) are estimated based on a panel Bayesian VAR model identified with contemporaneous restrictions. Cumulative impulse response functions are reported for real GDP growth, inflation and bank lending growth. All the variables are defined in percentage points. The median of the accepted draws is plotted together with the 32% and 68% Bayesian credibility bands.

5 Conclusion

There is little empirical evidence on how shocks to bank capital buffers affect the banking sector and the macroeconomy in the euro area. We fill in this gap by computing a measure of economic bank capital buffer at the country level for the four largest euro area countries. We find that shocks to economic bank capital buffers affect bank lending and also real GDP growth in these countries. These findings are important for the calibration and assessment of capital-based macroprudential policy measures, which are likely to affect the target capital ratio. In the case of policies which are countercyclical in nature, these results suggest that they could be useful for limiting the procyclicality and excessive amplification of the financial cycle, on top of helping to build resilience in the banking sector.

Box 1
A panel data econometric model to estimate economic bank capital buffers

It is assumed that banks adjust their capital ratios towards a pre-specified target economic capital ratio. However, owing to adjustment costs, a bank cannot adjust its actual capital ratio immediately. In particular, the change in the capital ratio in period t is assumed to depend on the gap between the target and the actual ratio in the previous period:

${T 1 C R}_{i, t} - {T 1 C R}_{i, t - 1} = γ ({T 1 C R}_{i, t - 1}^{*} - {T 1 C R}_{i, t - 1}) + ε_{i, t}$ (1)

where ${T 1 C R}_{i, t}$ and ${T 1 C R}_{i, t - 1}^{*}$ denote the observed and the target Tier 1 capital ratio respectively, $γ$ is the parameter driving the speed of adjustment and $ε_{i, t}$ is a bank-specific shock. The target economic capital ratio is unobserved and assumed to be a linear combination of bank ( $B_{i, t}$ ) and country-specific macroeconomic variables ( $M_{c, t}$ ):

${T 1 C R}_{i, t - 1}^{*} = α_{i} + θ_{B} B_{i, t} + θ_{M} M_{c, t}$ (2)

Since the target for the Tier 1 capital ratio is unobservable, it is not possible to estimate Equation (2) directly. Instead, the conjectured functional form (2) is substituted into Equation (1), as follows:

${T 1 C R}_{i, t} = γ ([α_{i} + θ_{B} B_{i, t - 1} + θ_{M} M_{c, t - 1} - {T 1 C R}_{i, t - 1}] - {T 1 C R}_{i, t - 1}) + ε_{i, t}$ (3)

Rewriting equation (3), it is possible to obtain:

${T 1 C R}_{i, t} = β_{0} + {β_{1} B}_{i, t - 1} + β_{2} M_{c, t - 1} + {β_{3} T 1 C R}_{i, t - 1} + ε_{i, t}$ (4)

where $β_{0} \equiv γ α_{i}$ , $β_{1} \equiv γ θ_{B}$ , $β_{2} \equiv γ θ_{M}$ and $β_{3} \equiv 1 - γ$ . Equation (4) is then estimated with bank-level fixed effects to obtain its coefficient estimates and to recover $\hat{γ}, \hat{α_{i}}, \hat{θ_{B}}$ and $\hat{θ_{M}}$ . These estimates are then used to construct the bank’s target for its capital ratio:

$\hat{{T 1 C R}_{i, t}^{*}} = \hat{α_{i}} + \hat{θ_{B}} B_{i, t} + \hat{θ_{M}} M_{c, t}$ (5)

With the individual target estimate, $\hat{{T 1 C R}_{i, t}^{*}}$ , it is possible to construct individual economic bank capital buffers:

${C B}_{i, t} = {T I C R}_{i, t} - \hat{{T 1 C R}_{i, t}^{*}}$ (6)

The buffers for the banks are then aggregated to obtain the aggregate economic bank capital buffer series for the euro area countries:

${C B}_{c, t} = {\sum_{i = 1}^{N} ω_{i, t - 1} C B}_{i, t}$ (7)

where $ω_{i, t - 1}$ denotes the share of bank i in the total assets at time t −1.

The calculation of the economic bank capital buffers is based on data from 18 systemically important euro area financial institutions. This is the largest number of financial institutions for which quarterly information on the Tier 1 capital ratio is available for a sufficiently long period of time. Stock price data are obtained from Bloomberg, while the Tier 1 ratio and total assets are obtained from Bloomberg, Bankscope, S&P CapitalIQ and SNL Financial. The source of the one-year ahead real GDP growth forecast is Consensus Economics, that of the sovereign bond yield spread is DataStream and that of the euro area aggregate corporate bond yield spread is the Federal Reserve Bank of St. Louis. The data spans the period from the first quarter of 2005 to the fourth quarter of 2018.

6 References

Aiyar, S., Calomiris, C.W. and Wieladek, T. (2014), “Does Macro-Prudential Regulation Leak? Evidence from a U.K. policy experiment”, Journal of Money, Credit and Banking, Vol. 46 (1), p.p. 181‑2014.

Babić, D. and Fahr, S. (2019), “Shelter from the storm: recent countercyclical capital buffer (CCyB) decisions”, Macroprudential Bulletin, ECB, Frankfurt am Main, March.

Bernanke, B.S. and Lown, C.S. (1991), “The Credit Crunch”, Brookings Papers on Economic Activity, No 2, Brookings Institution, p.p. 205‑239.

Berrospide, J.M. and Edge, R.M. (2010), “The Effects of Bank Capital on Lending: What Do We Know, and What Does It Mean?”, International Journal of Central Banking, Vol. 6, p.p. 5‑54.

Brewer, E., Kaufman, G.G. and Wall, L.D. (2008), “Bank capital ratios across countries: Why do they vary?”, Working Paper, No 2008‑27, Federal Reserve Bank of Atlanta.

Bridges, J., Gregory, D., Nielsen, M., Pezzini, S., Radia, A. and Spaltro M. (2014), “The Impact of Capital Requirements on Bank Lending”, Working Papers, No 486, Bank of England.

Budnik, K., Balatti Mozzanica, M., Dimitrov, I., Groß, J., Jansen, I., di Iasio, G., Kleemann, M., Sanna, F., Sarychev, A., Siņenko, N. and Volk, M. (2019), “Macroprudential stress test of the euro area banking system”, Occasional Paper, No 226, ECB, Frankfurt am Main, July.

Darracq Pariès, M., Fahr, S. and Kok, C. (2019), “Macroprudential space and current policy trade-offs in the euro area”, Financial Stability Review, ECB, Frankfurt am Main, May.

Francis, W., and Osborne M. (2009), “Bank Regulation, Capital and Credit Supply: Measuring the Impact of Prudential Standards”, Occasional Paper Series, No 36, UK Financial Services Authority, London.

Gropp, R. and Heider, F. (2008), “The Determinants of Capital Structure: Some Evidence from Banks”, Discussion Paper, No 08‑015, Centre for European Economic Research.

Gropp, R., Mosk, T., Ongena, S. and Wix, C. (2016), “Bank Response to Higher Capital Requirements: Evidence from a Quasi-Natural Experiment”, SAFE Working Paper Series, No 156, Goethe University, Frankfurt.

Hancock, D., Laing, A.J. and Wilcox, J.A. (1995), “Bank Capital Shocks: Dynamic Effects on Securities, Loans, and Capital”, Journal of Banking & Finance, Vol. 19, p.p. 661‑677.

Jiménez, G., Ongena, S., Peydro, J.-L. and Saurina, J. (2017), “Macroprudential Policy, Countercyclical Bank Capital Buffers, and Credit Supply: Evidence from the Spanish Dynamic Provisioning Experiments”, Journal of Political Economy, Vol. 125, p.p. 2126‑2177.

Kanngiesser, D., Martin, R., Maurin, L. and Moccero, D. (2017), “Estimating the impact of shocks to bank capital in the euro area”, Working Paper Series, No 2077, ECB, Frankfurt am Main, March.

Kok, C, Martin, R. Moccero, D. and Sandström, M. (2014), “Recent experience of European countries with macro-prudential policy”, Financial Stability Review, ECB, Frankfurt am Main, May.

Kok, C., Gross, M. and Zochowski, D. (2016), “The impact of bank capital on economic activity – Evidence from a mixed-cross-section GVAR model”, Working Paper Series, No 1888, ECB, Frankfurt am Main, March.

Lown, C. and Morgan, D.P. (2006), “The Credit Cycle and the Business Cycle: New Findings Using the Loan Officer Opinion Survey”, Journal of Money, Credit and Banking, Vol. 37(6), p.p. 1575‑1597.

Maurin, L. and Toivanen, M. (2012), “Risk, capital buffer and bank lending: A granular approach to the adjustment of euro area banks”, Working Paper Series, No 1499, ECB, Frankfurt am Main, November.

Meeks, R. (2017), “Capital Regulation and Macroeconomic Activity: Implications for Macroprudential Policy”, European Economic Review, Vol. 95, p.p. 125‑141.

Mésonnier, J.-S. and Monks, A. (2015), “Did the EBA Capital Exercise Cause a Credit Crunch in the Euro Area?”, International Journal of Central Banking, Vol. 11(3), p.p. 75‑117.

Mésonnier, J.-S. and Stevanovic, D. (2017), “The Macroeconomic Effects of Shocks to Large Banks’ Capital”, Oxford Bulletin of Economics and Statistics, Vol. 79(4), p.p. 546‑569.

Noss, J. and Toffano, P. (2016), “Estimating the Impact of Changes in Aggregate Bank Capital Requirements During an Upswing”, Journal of Banking and Finance, Vol. 62, p.p. 15‑27.

Peek, J. and Rosengren, E.S. (1997), “The International Transmission of Financial Shocks: The Case of Japan”, The American Economic Review, Vol. 87(4), p.p. 495‑505.

Stolz, S. and Wedow, M. (2011), “Banks’ regulatory capital buffer and the business cycle: Evidence for Germany”, Journal of Financial Stability, Vol. 7, pp. 98‑110.

Watanabe, W. (2007), “Prudential Regulation and the ‘Credit Crunch’: Evidence from Japan”, Journal of Money, Credit and Banking, Vol. 39(2‑3), p.p. 639‑665.

See, for example, Babić and Fahr (2019) and Darracq Pariès et al. (2019).
An insufficient number of observations makes it difficult to conduct this analysis for smaller euro area countries with a smaller number of banks.
These authors find that a one percentage point increase in capital requirements leads to an increase of 0.65 percentage points in the target capital ratio.
The requirements were always equal or greater than the Basel minimum of 8% and reflected supervisory judgments about risks not captured in the Basel capital framework, including the quality of bank management, corporate governance and systems and controls.
As a result, target economic capital ratios are different from capital requirements, although the latter can affect the target capital ratio, as mentioned before.
The use of partial adjustment models is standard in the literature. See Hancock et al. (1995), Berrospide and Edge (2010), Stolz and Wedow (2011) and Mésonnier and Stevanovic (2017).
Size is argued to capture complexity and agency problems. Profits capture the ability of banks to generate internal capital, and stock market volatility captures bank’s riskiness. See Gropp and Heider (2008) and Brewer et al. (2008).
Estimates are implemented using the BEAR Toolbox. The technique allows for country-specific coefficients, enabling differentiation of the impact of shocks across countries, and is identified via contemporaneous restrictions.
The monetary policy rate is the EONIA rate. Economic activity and inflation are the quarter-on-quarter growth rates of real GDP and headline inflation respectively. Bank lending is computed as the quarter-on-quarter growth rate of an index of notional stocks. Finally, bank lending spreads are the difference between interest rates on new business loans and the monetary policy rate.
Budnik et al. (2019) develop a macroprudential stress test for 91 institutions located in 19 euro area countries, lifting the static balance sheet assumption of supervisory stress test and allowing for a feedback loop to the macroeconomy. The authors find that banks deleverage in order to meet capital requirements in an adverse scenario.
The economic capital buffer may also change for other reasons, for example, due to a decline in the actual capital ratio. In this case, the impact may be even stronger if the actual capital ratio falls below regulatory requirements, because this breach may trigger automatic restrictions on distribution of even liquidation.

Vai jūs apmierina šīs lapas darbība?

Jā Nē

The macroeconomic impact of changes in economic bank capital buffers

1 Introduction

2 Challenges in estimating the impact of changes in bank capital buffers